Doodling Shake Bot DIY STEM Kit
$9.99$4.95
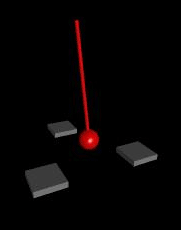 For example, imagine an equilateral triangle made of wood with a strong magnet, positive
pole facing up embedded at each vertex. suspend a magnet with negative pole facing down
by a string exactly over the center of the triangle. If you move the pendulum to any
point and then release it, the pendulum magnet will come to rest over one of the embedded
magnets due to their mutual attraction. This simple physical system can be completely
described by a few equations relating momentum, gravitational force, magnetic force, air
resistance and such, and so you would think if you measured where the pendulum was before
release you could accurately predict which of the 3 vertices it would end up with. But
not so;
For example, imagine an equilateral triangle made of wood with a strong magnet, positive
pole facing up embedded at each vertex. suspend a magnet with negative pole facing down
by a string exactly over the center of the triangle. If you move the pendulum to any
point and then release it, the pendulum magnet will come to rest over one of the embedded
magnets due to their mutual attraction. This simple physical system can be completely
described by a few equations relating momentum, gravitational force, magnetic force, air
resistance and such, and so you would think if you measured where the pendulum was before
release you could accurately predict which of the 3 vertices it would end up with. But
not so;